Jeff Hawkins: Brain science is about to fundamentally change computing

Jeff Hawkins is the founder of Palm Computing, he invented the Palm Pilot. Nowadays he work on neuroscience. This is a great presentation about Brain Theory.

Garrett Lisi: A beautiful new theory of everything

Antony Garrett Lisi is a theoretical physicist best known for “An Exceptionally Simple Theory of Everything”. This TED talk is about that theory. Garrett explains how he find this theory. Garrett Lisi has proposed this new “theory of everything” a grand unified theory that explains all the elementary particles, as well as gravity.

Hylomorphisms in Haskell

If you miss something in this post, I suggest you to start in Catamorphisms and Anamorphisms.

A Hylomorphism is just the composition of one catamorphism and then one anamorphism.
, replacing that by the proper notation we have:

In this post I will use the structure of a binary tree:

data BTree a = Empty | Node(a, (BTree a, BTree a))

I will use the tuples to don’t have to write uncurry’s. As I will show you, when we say that we are making a hylomorphism on a particular data type , what we are trying to say is that the intermediate structure of our combination of catamorphism and anamorphism is that data type . This is the structure throw our morphism will communicate with each other.

Anamorphism

So, here I will solve the Quicksort algorithm with a hylomorphism over .

The intermediate structure being a doesn’t mean that my function will receive . My function works over lists. So the first thing to do, is draw the respective anamorphism from to :

My strategy here is to do all the work in the anamorphism, so, I need a function with type:
, or in Haskell

That function is :

qsep :: [a] -> Either () (a, ([a], [a]))
qsep []    = Left ()
qsep (h:t) = Right (h,(s,l))
    where (s,l) = part (<h) t

part:: (a -> Bool) -> [a] -> ([a], [a])
part p []                = ([],[])
part p (h:t) | p h       = let (s,l) = part p t in (h:s,l)
             | otherwise = let (s,l) = part p t in (s,h:l)

This code is very simple, in I chose a pivotal element (first one), and filter the bigger to one side, and the other ones to the other, just like the algorithm. The function that do all that job is , it process all the list finding the elements that satisfy the condition , to put them in the left side of the tuple, and the others into the right side.

This function by it self don’t do almost anything, it is only a simple part of the algorithm.

Catamorphism

Next step is to see the diagram for catamorphisms from to :

As I said before, the heavy duty is on the side of the anamorphism, so here, the catamorphism will be very very simple. In fact it is.

inord :: Either a (a, ([a], [a])) -> [a]
inord = either (const []) join
    where join(x,(l,r))=l++[x]++r

That right! The only thing that the catamorphism do is a inorder passage over the structures , which is very simple, as as shown by the code.

Hylomorphism

The first thing is to draw the diagram, now for the hylomorphism, the composition of the cata with the ana:

Once having made the two most important parts of the function (the ana and cata), the hylo is very simple to do. You just have to make a function :

hyloBTree h g = cataBTree h . anaBTree g

And our function bacame:

qSort :: Ord a => [a] -> [a]
qSort = hyloBTree inord qsep

And that’s it, now I’m going to show you the all code that you need to put all the things together and working.

inBTree :: Either () (b,(BTree b,BTree b)) -> BTree b
inBTree = either (const Empty) Node

outBTree :: BTree a -> Either () (a,(BTree a,BTree a))
outBTree Empty              = Left ()
outBTree (Node (a,(t1,t2))) = Right(a,(t1,t2))

baseBTree f g = id -|- (f >< g))

cataBTree g = g . (recBTree (cataBTree g)) . outBTree

anaBTree g = inBTree . (recBTree (anaBTree g) ) . g

hyloBTree h g = cataBTree h . anaBTree g

recBTree f = baseBTree id f

Outroduction

If you need more explanations feel free to contact me.

Catamorphisms in Haskell

Lately I have had many works to do at university, therefore I’m sorry for the non regularity of my post’s.
By the way, I also liked to announce that this is my first conscientious post at Planet Haskell.

Why Catamorphisms and Point-Free

Catamorphisms is the way that we can explain in one function how recursive patterns works in some data type.
Here I will use Point-Free notation because what matters here is to show the data flow and the composition of functions.
Point-Free style is used to think in data flow terms, and very useful to program verification, applying formalism to our code.

In point-free style of programming programs are expressed as combinations of simpler functions. This notation is known as write functions without their arguments. Pointwise is the normal form how we write a function.

Couple of examples of point-free notation:
1)

sum = foldr (+) 0 -- point-free
sum l = foldr (+) 0 l -- pointwise

2)

f = (*10).(+2) -- point-free
f n = (n+2)*10 -- pointwise

Clarifications

First of all to define a function, for example , I say:

or
or

I will assume that you are familiarized with infix notation, , , and composition function.

Types

In Haskell we have this definition for lists:

data [a] = [] | a : [a]

Let’s create the same, but more convenient. Consider the following isomorphic type for lists:

data List a = Empty | Node(a,List a) deriving Show

To represent we wrote .

As you can see, to construct a we have two options, or . Formally we represent the constructor as . And we use to say that our two possibilities are or . We could see as a the following function:

Node :: (a,List a) -> List a

So typologically we have . We use to define that two things occurs in parallel, like tuples do, so we can redefine it:

Now we can say that is isomorphic to .
This is something to say that and keep the same information without any change or any loss.

Catamorphisms as composition of functions

Let , , , be Inductive data types (sets) and , , functions.

We will write using the composition of , , functions. That way we are breaking our problem in small ones. So, in the end we will have the following definition for :

The function that we want is , and that function is over so we have:

cata :: (D -> C) -> List a -> C

Type is . Maybe this isn’t clear yet, let’s start with function

out

The function is responsible to create the isomorphism between and , so the code could be something like this:

outList :: List a -> Either () (a,List a)
outList Empty    = Left ()
outList (Node t) = Right t

In Haskell we represent the type as , as and as .

So, type is .

function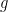

The function is also known as *gen*, here is where we said the step that pattern do. Imagine that we want to insert all the values of into :

-- pointwise
g :: Either () (a,[a]) -> [a]
g (Left()) = []
g (Right(a,h)) = a:h

-- pointfree
g = either (const []) (uncurry (:))

We represent as .
Now we can be more specific with our graphic:

rec

Here we have to get a function that transform into . That function, general rec, will be:

recg f g h = f -|- (g ><  g) x = ((f . fst) x , (g . snd) x)

With that function we can say exactly what to do with type , , and in domain of .
So we want something like this:

rec g = recG id id g

like that we said that will be the same in the counter domain of . Now we need a function that receive a and give us a …
Yes, that function is ! So, the final graphic became:

cata

Finally we gonna to define the function :

cata g = outList . rec (cata g) . g

where is our *gen* function,

g = either (const []) (uncurry (:))

And our objective:

List2HaskellList = cata $ either (const []) (uncurry (:))

More catamorphisms

Imagine we have the following data type:

data NList a where
    Leaf  :: a -> NList a
    NNode :: a -> [NList a] -> NList a

, , and became:

out (Leaf a) = Left a
out (NNode a l) = Right (a,l)

Using the previous definitions of and

rec f = id -|- (id >< map f)

cata g = g . rec (cata g) . out

Imagging that has type:

g :: Either a (a,[[a]]) -> [a]

And the graphic for this cata became:

Conclusion

I’ve talked about cata’s without any formalism, the idea was to explain to someone who didn’t know.

I will talk more about catamorphisms and how to calculate programs with them.
In the future I will like to talk about anamorphisms too. And Later on I will talk about point-free over non recursive functions.